The Problem: While scRNAseq has revolutionised how we see cellular heterogeneity, we've lacked principled methods to transform these high-dimensional snapshots of gene expression into predictive models that explain HOW cells make decisions Most approaches describe what we see, not how it happens
Solution: Dynamic Landscape Analysis (DLA) - a framework rooted in dynamical systems • Identifies stable cell states as "attractor clusters" • Maps transition pathways between states • Builds predictive mathematical models
Key Innovation: Getting beyond descriptive trajectories. DLA generates a geometric dynamical model—a Waddington landscape—that provides mechanistic insights without needing every molecular detail It bridges microscopic gene expression to macroscopic cell behaviour
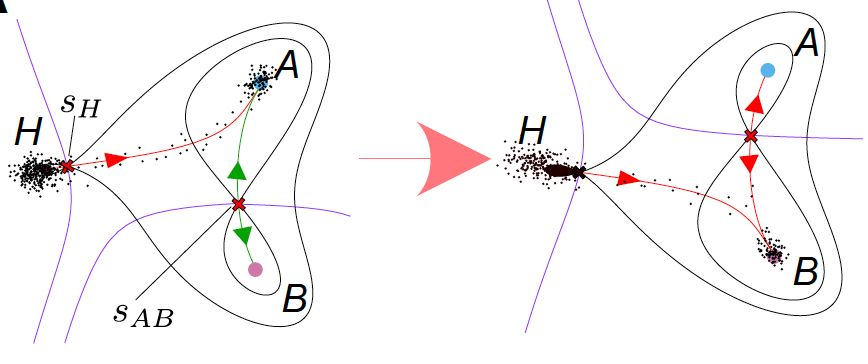
Classifying Decisions: We identified three types of cell fate decisions, each governed by distinct dynamical bifurcations: • Direct transitions (fold bifurcations) • Binary flip decisions • Binary choice decisions These mathematical structures explain how signalling controls cell fate allocation
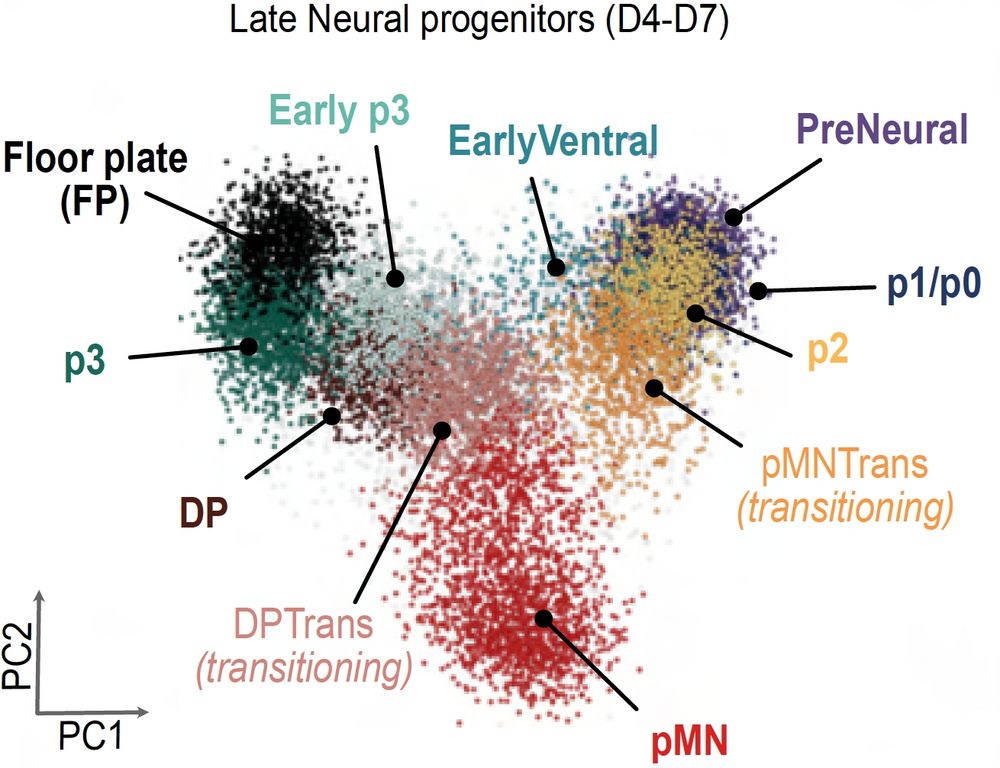
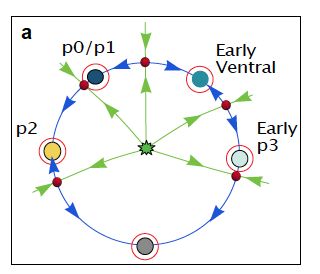
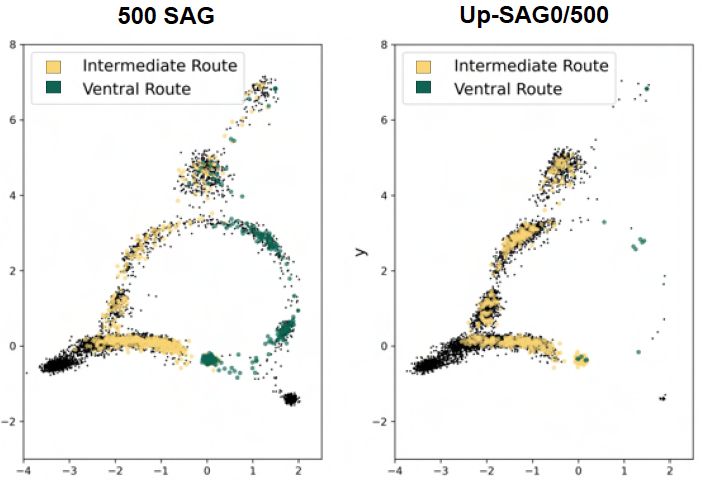
Surprising Finding: Studying neural tube differentiation, we discovered an unexpected circular topology Cells that initially diverge into different lineages can converge through multiple routes to the same fate This challenges the traditional "branching tree" view of development
Predictive Power: The model successfully predicts cellular responses to signalling conditions not seen before When we tested new patterns of Sonic Hedgehog signalling experimentally, the predictions matched xpts This is true predictive biology, not just curve fitting
@amartinezarias.bsky.social you're going to love this one
Cross-Species Validation: Applying DLA to human neural organoids revealed conserved decision-making principles between mouse & human The mathematical structure underlying cell fate decisions appear to be fundamental features of vertebrate neural tube development
Broader Implications: Readily applicable to many single-cell datasets with potential for generative & explanatory models Intriguing parallels to machine learning - both progress through critical decision points. Foundation of decision-making in complex systems? See: journals.aps.org/prresearch/a...
Credits: It was a long & intense project. All credit to Marine Fontaine (maths) & Joaquina Delas (xpts) for driving it forward. Supported by Meri Saez, Lizzie Finnie, and Rory Maizels It's the result of a longstanding collaboration with David Rand Preprint: www.biorxiv.org/content/10.1...
📌
This is extremely interesting. Could this be related to the core finding from @ldelvalleanton.bsky.social @borrell-lab.bsky.social’ study? www.science.org/doi/10.1126/...
Could be, although we suspect that newborn neurons that are transcriptomically very similar (clustered) may be epigenomically distinct.
Thanks Victor
Not to get overexcited, but I think we've got some of those 'not in my lifetime' findings coming in at last. Waddington would love this. I met him once. He was old. I was young and somewhat overawed. Even though I knew what 'homeorhesis' meant, I didn't ask him any of the questions I should have.